今回は、自立式鋼矢板土留め壁について1/βを考えてみようと思います。
道路土工 仮設工指針には以下の記載があります。チャン(chang)の式ですね。loは根入れ長で、βは杭の特性値です。

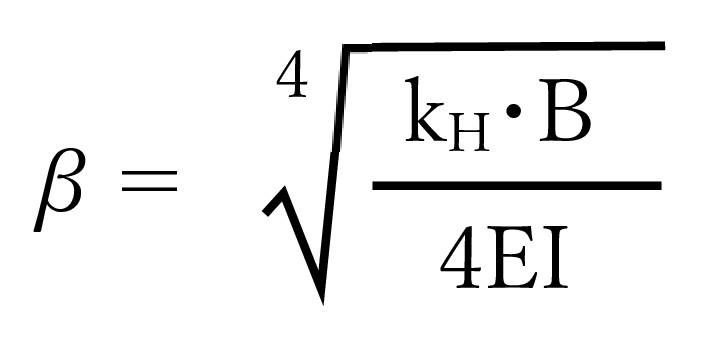
そして、βの式中のKHは水平地盤反力係数ですが、仮設工指針には「通常、1/βの範囲の平均値」と記載があります。
この1/βとはどういったものなのかを今回は考えてみようと思いました。
水平地盤反力係数が1/βの範囲ということは、なんとなくイメージとして鋼矢板が土留めで支えている土圧などの水平力を、根入れ部分の鋼矢板が横抵抗で支えている部分として有効な深さが1/βなのかと想像はできるとは思います。
杭の水平力による曲げの現象に対して道路橋示方書に記載のある杭の深さ方向の挙動に関するさまざまな公式でどの値が近いものとなるかを計算してみることにしました。
計算条件
今回の計算は以下の条件で行うことにします。鋼矢板はⅢ型とします。
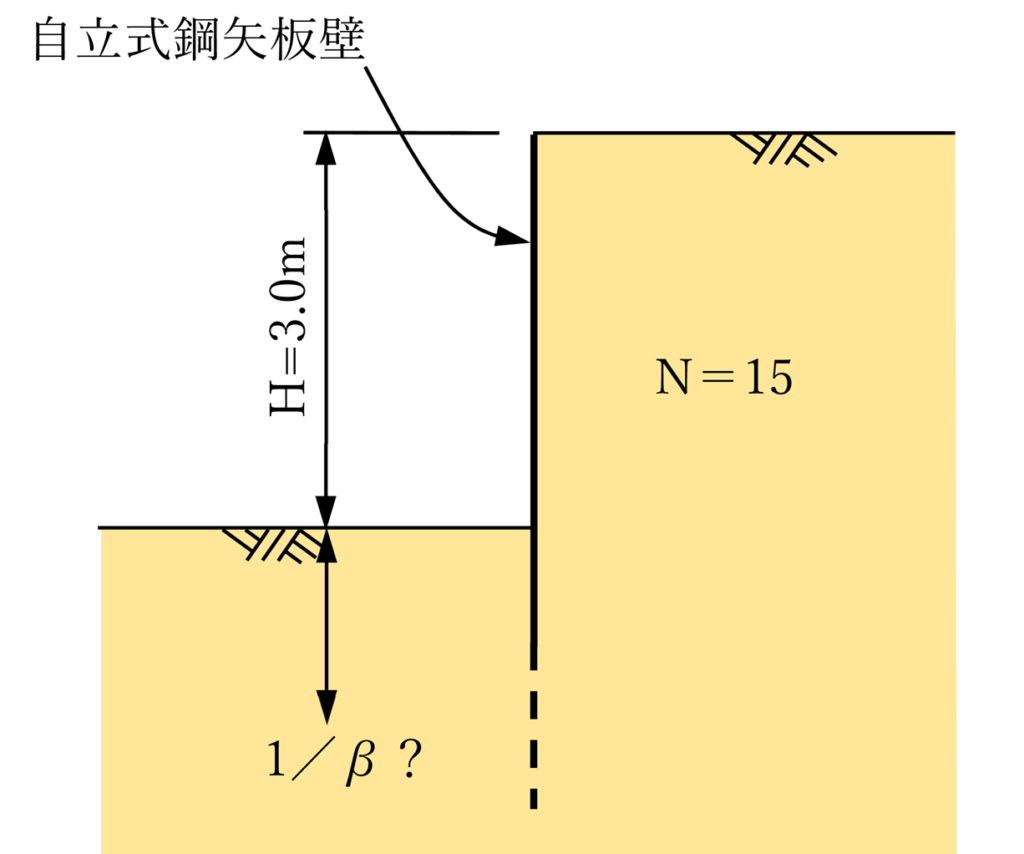
βの算出
上記の条件でまずβを計算してみます。鋼矢板は計算の結果、β=0.5236 となりました。


杭の一般式と計算ケース
杭の挙動の一般式として道路橋示方書に記載のある下記の3項目を計算してみようと思います。
① lm:杭の最大曲げモーメントが生じる地点の深さ
② l:杭のひずみの第一不動点となる地点の深さ
③ L:杭のたわみ角が0となる深さ
また、計算モデルのケースとして以下の3つがあります。
① 基本系(杭頭M作用)
② 杭頭M=0
③ 杭頭が回転しない場合
計算結果
①基本系は今回計算条件の土留め壁天端に曲げを作用させていないのでM=0としました。従いまして、①と②杭頭M=0の両ケースは同じ計算結果になりました。土留めの計算ケースとしては①と②が該当すると思います。とりあえず今回ケースは②としましょう。③は参考に計算しました。
計算結果の値を見ますと1/βが1.910mですがそれに一番近い値としてl=1.952mとなりました。これは「ひずみの第一不動点の深さ」となりますね。ということは、これより浅い位置では水平力に対して杭は土と共に横抵抗を発揮する範囲であり、これより深い位置ではひずみが反対側に変位するので、水平力に対抗する方向への横抵抗は期待できないということでしょう。Ⅱ型やⅣ型の鋼矢板でも同様の計算をしましたが、同じようになりました。
ちなみに①ケースで杭頭曲げが生じたり③ケースの場合では1/βと各値が近似しないので、注意が必要であると思います。
| 杭の状態 | ①基本形(杭頭M作用) | ②杭頭M=0 | ③杭頭が回転しない場合 |
| たわみ曲線 曲げモーメント図 (道路橋示方書より引用) |
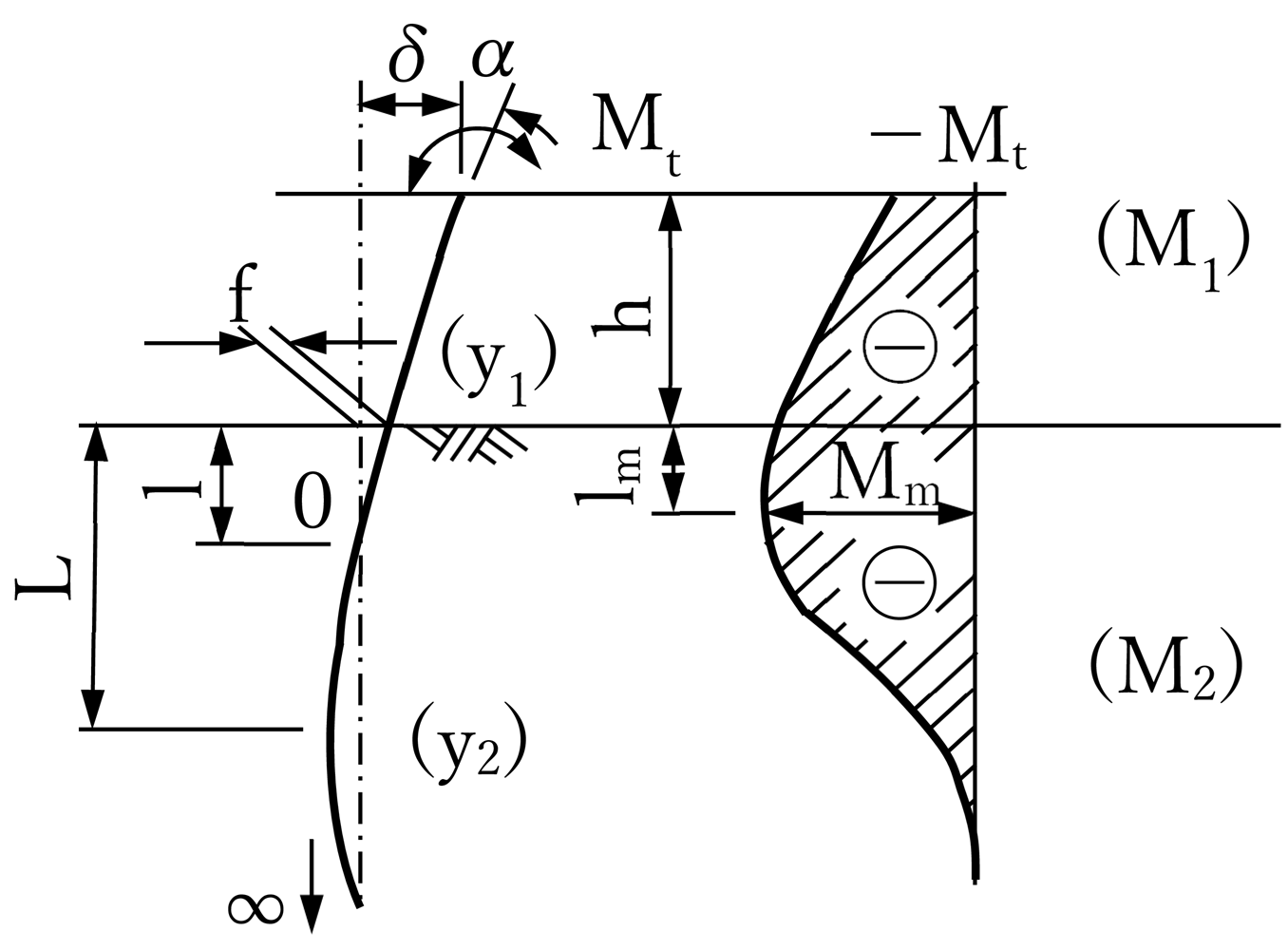 |
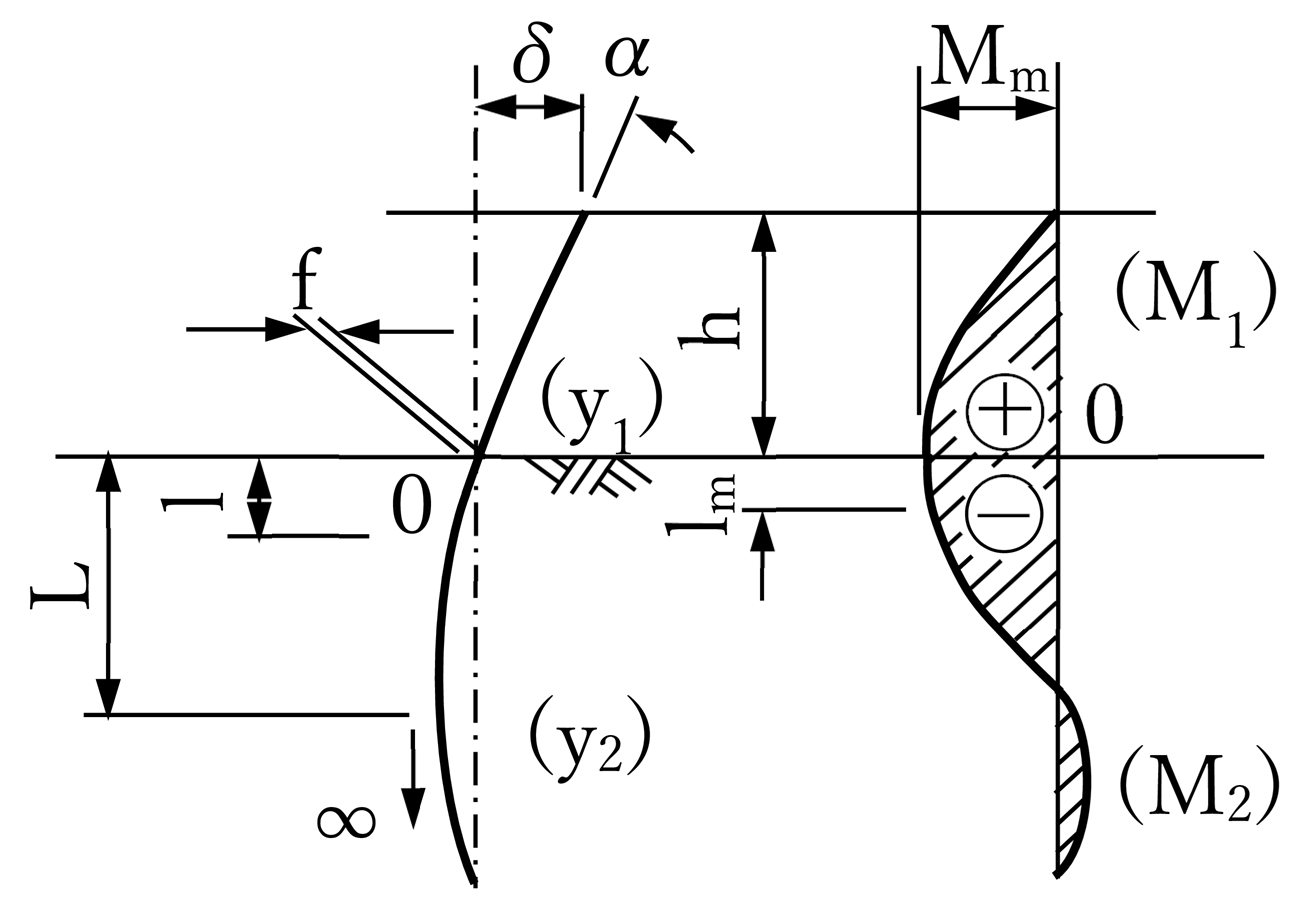 |
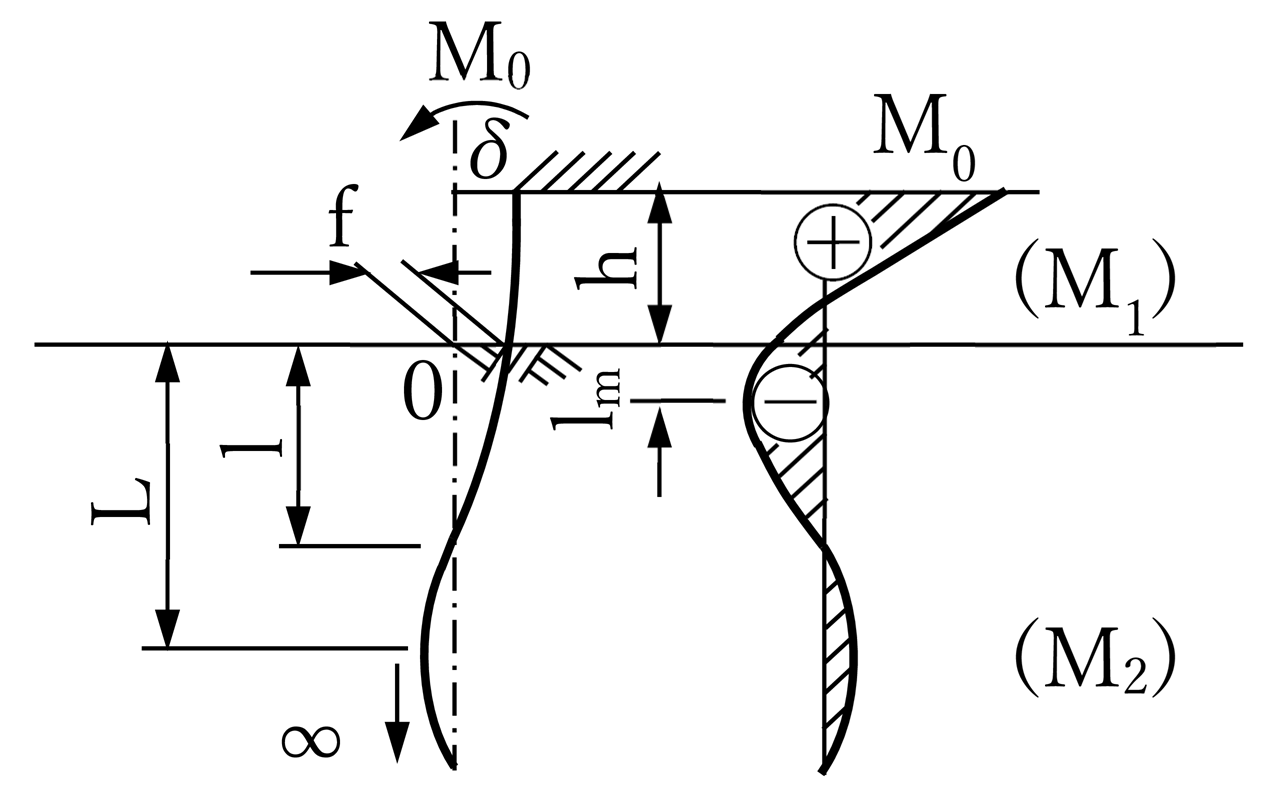 |
| 公式(道路橋示方書より引用) lm:最大曲げモーメントの深さ l:ひずみの第一不動点の深さ L:たわみ角0となる深さ 単位(m) |
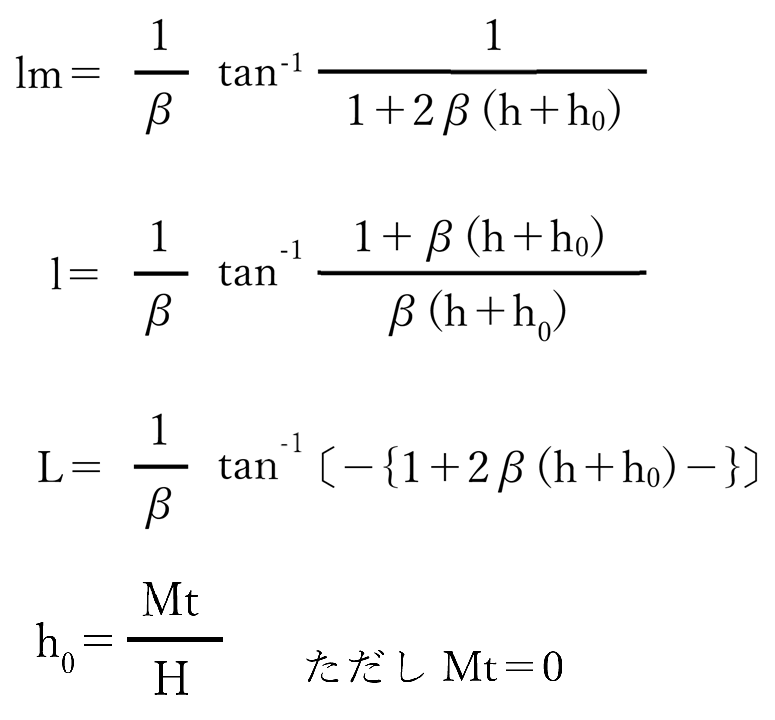 |
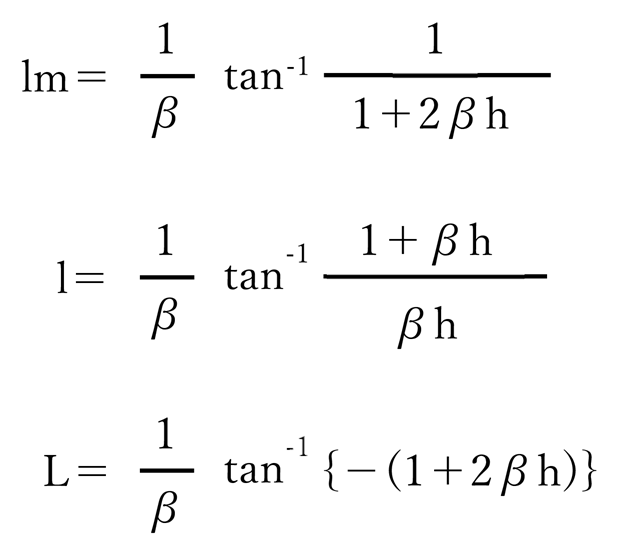 |
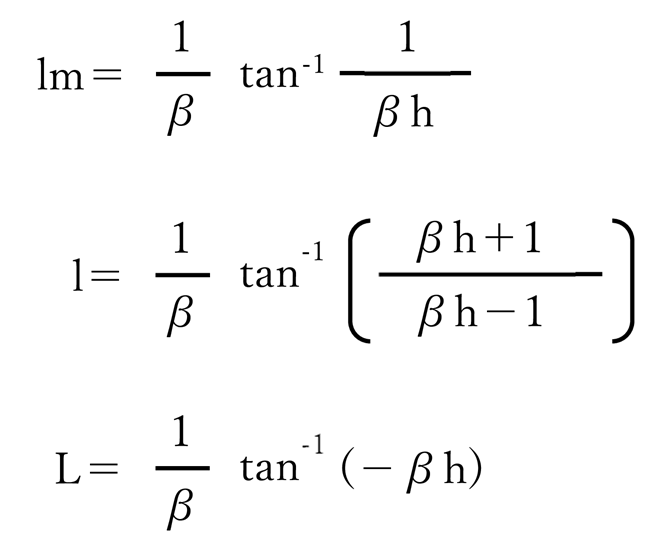 |
| β | 0.5236 | 0.5236 | 0.5236 |
| 計算結果 1/β(m) | 1.910 | 1.910 | 1.910 |
| ①計算結果 lm(m) | 0.452 | 0.452 | 1.083 |
| ②計算結果 l(m) | 1.952 | 1.952 | 2.583 |
| 計算結果L (m) | -2.548 | -2.548 | -1.917 |
まとめ
今回は出版されている書物に沿って計算を行ったものであり、その計算結果や仮設工指針にある「水平地盤反力係数は1/βの範囲の平均値」と記載によることから、横抵抗を発揮する範囲であろうと思うところであります。また余談ですが、同じく仮設工指針に記載の根入れ長の式である2.5/βはそれ以上深く入れても曲げやひずみが発生せず効果が変わらない(水平力に対して)という範囲であると思います。それは、道路橋示方書では「βLc≧3を半無限長の杭」としており仮設工指針では仮設なので2.5としているのだと思いますが同様に半無限長の杭の理論であると思うことからです。
仮設工指針の1/βはどういう意味があるということが記載されている書物は私が見た限りありません。上表の公式ではどれも1/βが含まれていて、それにアークタンジェントの式を乗じていることを考えると1/βと同じではないことが分かります。正確には「l」ということかもしれませんが近い値として1/βとしても差し支えないと私は理解しました。ここに少し曖昧さがあることからしっかりと1/βの意味を記載する書物がないのかもしれません。



コメント